Last time¶
- Introduction to (quantum) complexity theory
- BQP: polynomial time quantum computation
- BQP $\subseteq$ PSPACE
BQP vs NP?¶
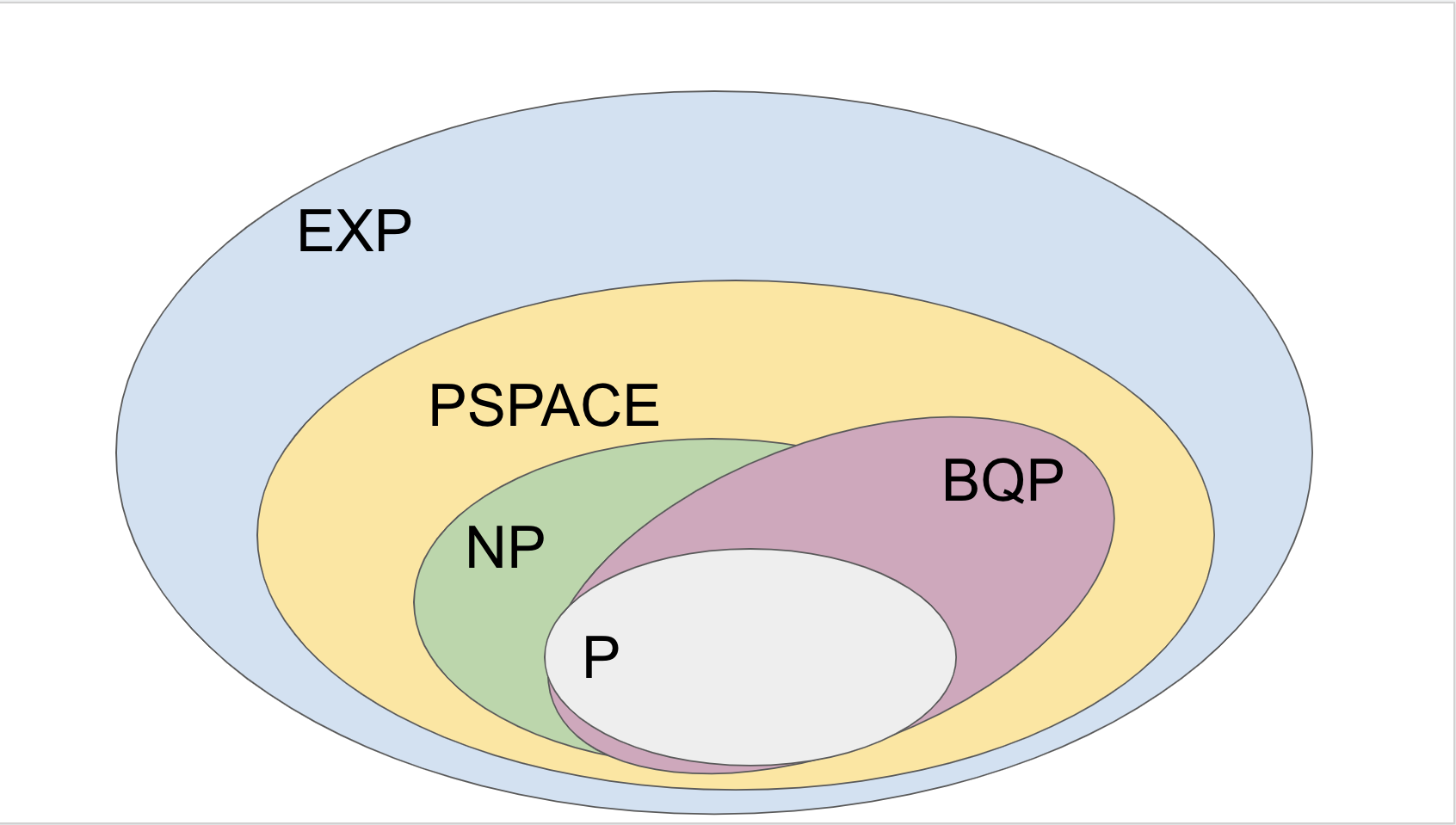
NP - Nondeterministic Polynomial Time¶
Decision problems where the "yes" inputs have solutions that can be efficiently checked.
Example: Traveling Salesman Problem
Input: Graph $G$, integer $k$
Output: Does $G$ have a tour of length at most $k$ that visits every city once and returns to origin?
TSP is in NP because given a proposed tour, one can check whether it visits every city once, returns to origin, and has length at most $k$.
NP - An equivalent definition¶
A decision problem has an NP "algorithm" if the algorithm can nondeterministically guess a solution (if it exists), and check the solution in polynomial time. If there is no solution, no guess will be accepted.
A common misconception¶
"Quantum computers solve problems by trying all possible solutions simultaneously and outputting a correct one!"
If that were true, then NP complete problems would be instantly solvable on quantum computers.
However this simplistic picture of quantum computing is not true. The truth is much more interesting...
Evidence that NP $\not\subseteq$ BQP¶
We don't have the tools available to outright prove that BQP cannot solve NP-complete problems. But we can try to give evidence for this.
We will show a black box separation (also known as oracle separation between NP and BQP.
Computing with Black Boxes¶
Decision problems are defined with inputs that are represented as binary strings (i.e. graphs, integers, etc. are represented in binary), and the outputs are about whether the inputs satisfy some property.
In the oracle model, decision problems get black box functions as input, and the goal is to decide something about the function given query access to the function.
In particular, cannot "look inside the black box" in order to solve the problem.
Unstructured search problem¶
Input: A black box function $f: \{0,1\}^n \to \{0,1\}$.
Output: Does there exist $x$ such that $f(x) = 1$?
Unstructured search problem¶
There is an NP oracle algorithm that "solves" the Unstructured Search Problem with $1$ query.
If there is a solution $x$, the NP oracle algorithm guesses $x$ and queries $f$ to see check if $f(x) = 1$.
Unstructured search problem¶
There is an quantum oracle algorithm (namely, Grover's algorithm) that solves the Unstructured Search Problem with $O(\sqrt{2^n})$ quantum queries.
Question: is there a quantum algorithm that can solve Unstructured Search Problem with $\mathrm{poly}(n)$ queries?
Lower bound on unstructured search¶
Bennett, Bernstein, Brassard, and Vazirani: "Strengths and weakness of quantum computing" (1997)
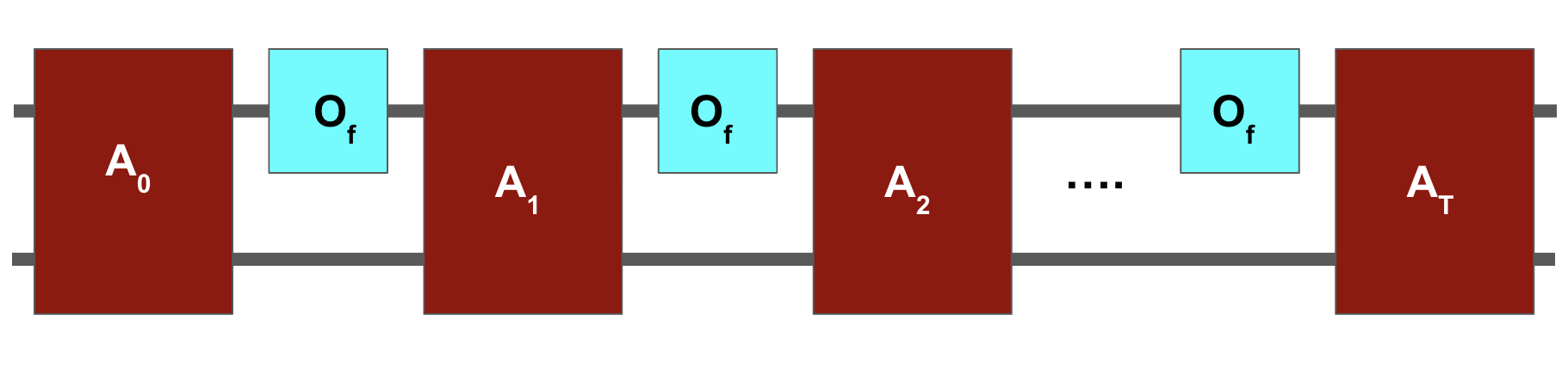
Suppose there was a quantum algorithm $A$ that could find a marked input to $f:\{0,1\}^n \to \{0,1\}$ using $T \ll \sqrt{2^n}$ queries to $O_f$.
We will show that $A$ can't increase the amplitude on the marked input fast enough to notice it.
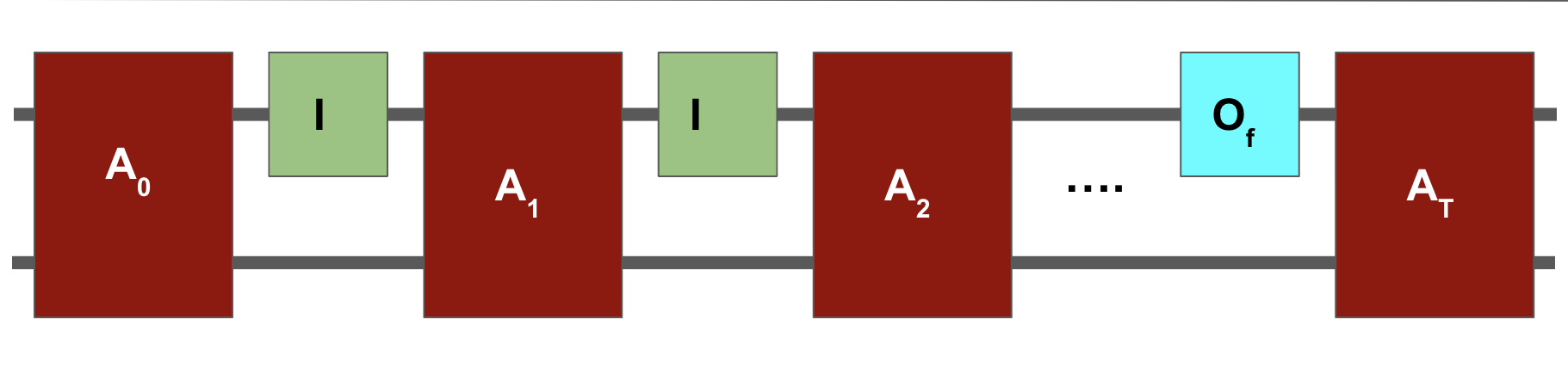
Modeling the algorithm¶
The algorithm $A$ alternates between fixed unitaries $A_0,A_1,\ldots,A_T$ that don't depend on $f$, and phase oracles $O_f$.
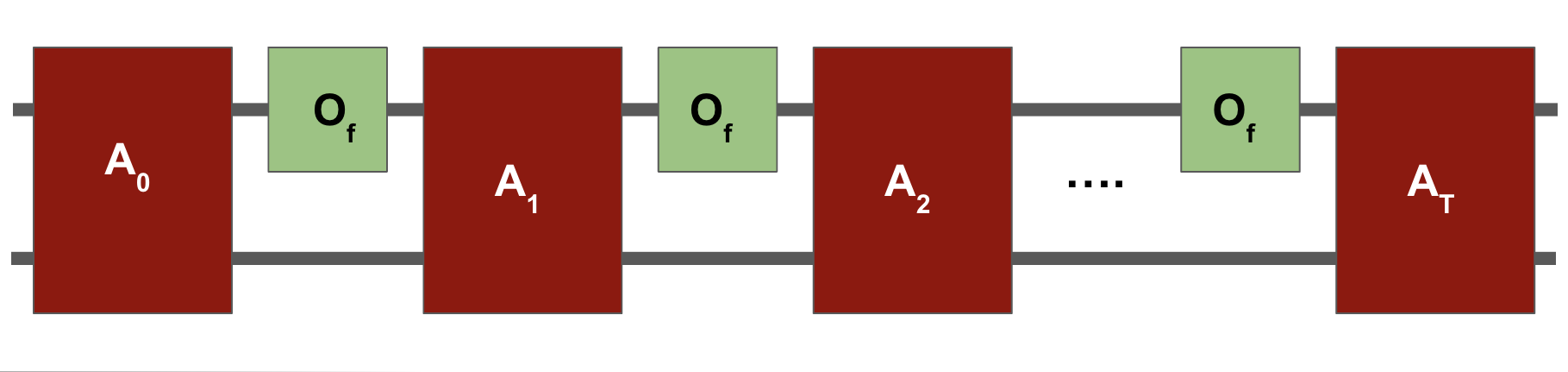
It starts in the all zeroes state, and either outputs a marked input $\ket{x^*}$ with high probability or outputs "NO MARKED INPUT".
Hybrid method¶
Imagine running the algorithm $A$ on the all zeroes function (there is no marked input).
This is equivalent to running the algorithm with the phase oracle $I$.
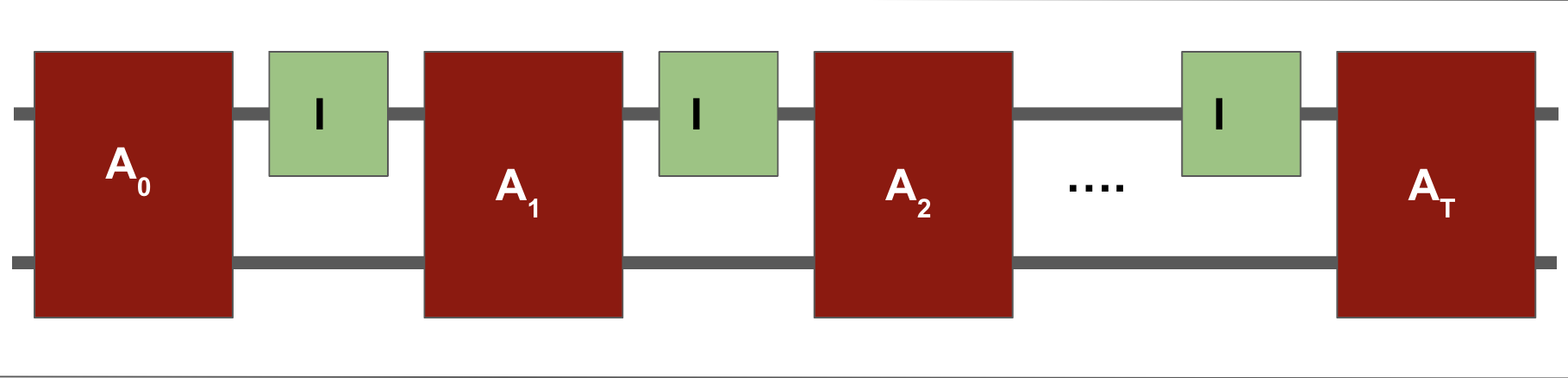
Let $\ket{\psi_T^I}$ denote the final state of the algorithm. Measuring it yields "NO MARKED INPUT" with high probability.
Goal: Show there exists $f(x)$ with unique solution $x^*$, where running $A$ with $O_f$ yields output state $\ket{\psi^f_T}$ satisfying
$$ \Big \| \ket{\psi_T^I} - \ket{\psi^f_T} \Big \| \leq O(T/\sqrt{2^n}) \ll 1. $$Contradiction: measuring $\ket{\psi^f_T}$ yields "NO MARKED INPUT" with high probability.
Identifying "overlooked" input¶
Define $\ket{\psi^I_t}$ = state of algorithm querying $I$ right after $t$'th query, for $1 \leq t \leq T$.
Intuition: There has to be an $x^*$ where the total amplitude over all timesteps is small.
Identifying "overlooked" input¶
Define the query magnitude of $x \in \{0,1\}$
$$ M_x = \sum_{t=1}^T \sum_w |\alpha_{t,x,w}|^2. $$Claim: $\sum_x M_x = T$
Proof:
$ \sum_x M_x = \sum_{t=1}^T \sum_{x,w} |\alpha_{t,x,w}|^2$ (by definition of $M_x$)
$ \qquad = \sum_{t=1}^T 1$ (because $\ket{\psi_t^I}$ is a unit vector)
$\qquad = T$.
Identifying "overlooked" input¶
Therefore there exists $x^*$ where $M_{x^*} = T/2^n$.
Define $f(x)$ to have $x^*$ as a unique solution.
This $x^*$ is an "overlooked" input - it does not get a lot of attention from the algorithm!
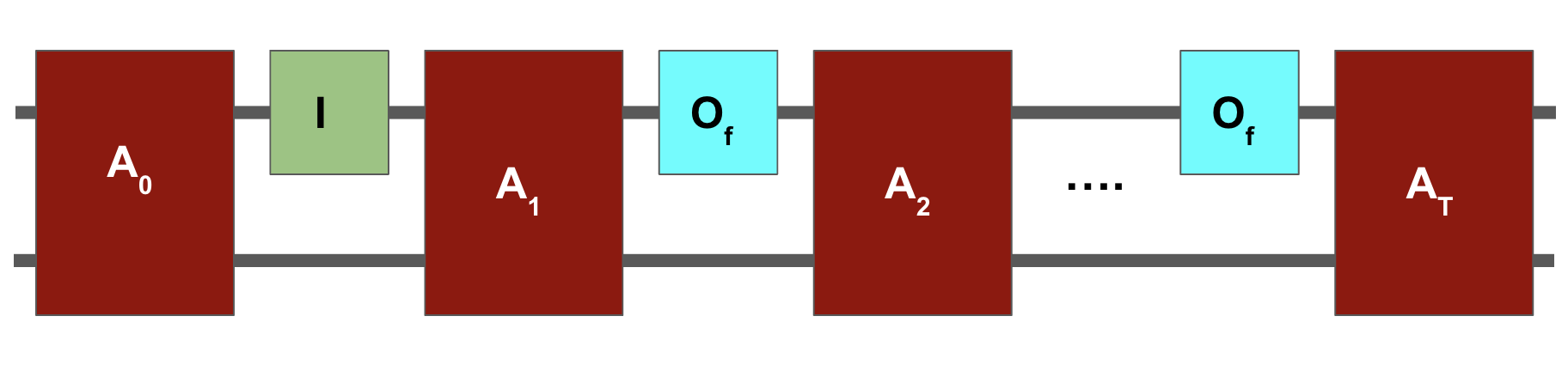
Hybrid method¶
To show that $\ket{\psi_T^f}$ is close to $\ket{\psi_f^I}$, we analyze hybrids, which are fictitious runs of the algorithm where the oracle changes in the middle.
Hybrid 0: all $T$ queries to $I$.
Hybrid 1: first $T-1$ queries to $I$, last query to $O_f$.
Hybrid $k$: first $T - k$ queries to $I$, last $k$ queries to $O_f$.
Hybrid method¶
Analyze on the board.
We're still far away from being able to run Grover's algorithm or Shor's factoring algorithm. How to demonstrate quantum advantage in the near term?
Quantum supremacy task¶
We wish to find a computational task $T$ that:
- NISQ (Noisy Intermediate-Scale Quantum) machine can run $T$ in, e.g. < 1 second.
- Verifiable on a classical computer in a reasonable amount of time (e.g. several weeks on a supercomputing cluster)
- Some complexity evidence that $T$ cannot be efficiently solved by classical computers.
Such a task $T$ would demonstrate the supremacy of quantum computers over classical computers.
Quantum supremacy task¶
This computational task $T$ can only happen in a "sweet spot" with $\sim 50$-$100$ qubits.
Enough that it's not easy for classical computers, but not too much so that we can run it on our existing quantum computers, and also verify it using $\sim 2^{50}$ operations on a classical computer.
Random circuit sampling¶
Number of qubits $n = 50$
Number of gates $m = 200$
Number of samples $T = $ several million
- Pick a random quantum circuit $C$ acting on $n$ qubits, with $m$ gates.
- Using quantum computer run circuit $C$ on $\ket{0 \cdots 0}$, generate samples $x_1,\ldots,x_T$ from the distribution $\mathcal{D}_C$.
- Output $x_1,\ldots,x_T$.
The distribution $\mathcal{D}_C$: each sample $x$ occurs with probability $p_C(x) = |\bra{x} C \ket{0 \cdots 0}|^2$.
Hardness of random circuit sampling?¶
A quantum computer, by definition, can easily perform the random circuit sampling task. How hard is it for a classical computer to do the same?
Theorem (Bouland, Fefferman, Nirkhe, Vazirani): There is no classical algorithm that, given circuit $C$, can generate samples from $\mathcal{D}_C$ with high probability, unless the polynomial hierarchy collapses to the third level.
Hardness of circuit sampling¶
"X unless the polynomial hierarchy collapses" is complexity theory evidence that X is true. It is a generalization of the assumption that $P \neq NP$.
This theorem talks about sampling exactly from $\mathcal{D}_C$. However, not even the quantum computer can do that, because it has some small amount of noise. One can ask how hard is it to approximately sample from $\mathcal{D}_C$. It is conjectured that this is still hard for classical algorithms (assuming polynomial hierarchy does not collapse).
Verification of random circuit sampling¶
How do you check whether a bunch of samples $x_1,\ldots,x_T$ were generated by $\mathcal{D}_C$? There is no known efficient way of doing so.
Idea: Heavy output generation (HOG) test
- Use a classical supercomputer to compute the median $\alpha$ of all $p_C(x)$.
- If at least $2/3$ of $x_1,\ldots,x_T$ are heavy (meaning $p_C(x_i) \geq \alpha$), then accept. Otherwise reject.
Verification of random circuit sampling¶
Intuition: heavy $x$'s form the bulk of the probability mass of distribution $\mathcal{D}_C$. Sampling from $\mathcal{D}_C$ should yield a lot of heavy strings.
However, it should also be hard for a classical computer to predict, given a circuit $C$ and $x$, whether $p_C(x)$ is above the median.
If a quantum machine is able to consistently output heavy strings from $\mathcal{D}_C$, then the machine must've "done something right".

Google Experiment¶
Conducted in Fall 2019. Ran many circuits on their 49-qubit "Sycamore" chip.
Extremely noisy: signal-to-noise ratio is about 1%. (However, Google claims it is enough to verify the sampling).
Recently: many challenges to this claim (faster classical simulations, noisy sampling may not be as hard as we thought).
Next time¶
Simulating quantum physics.