Admin¶
- Pset3 out, due November 2
- Henry, please record the lecture!
Quantum computing, so far¶
- Simons Algorithm
- Quantum Fourier Transform, Phase Estimation, Order Finding
- Grover Search, Quantum Counting, Amplitude Amplification
Nearly 30 years after Shor's and Grover's algorithm, we still only have a very murky idea of when quantum computers are better than classical computers.
The formal study of this question is the focus of quantum complexity theory.
Computational complexity theory¶
Study of various computational resources needed to solve computational problems.
- time
- space
- interactivity
- randomness
- non-determinism
- quantumness
- ...
Computational complexity theory¶
The central questions:
- How do these computational resources relate to each other?
- What are the tradeoffs?
- Does non-determinism help speed up computations (P vs NP)
- If a problem can be solved using a small amount of memory, can it also be solved using a small amount of time?
- Can quantum computers efficiently solve problems that are hard for classical computers?
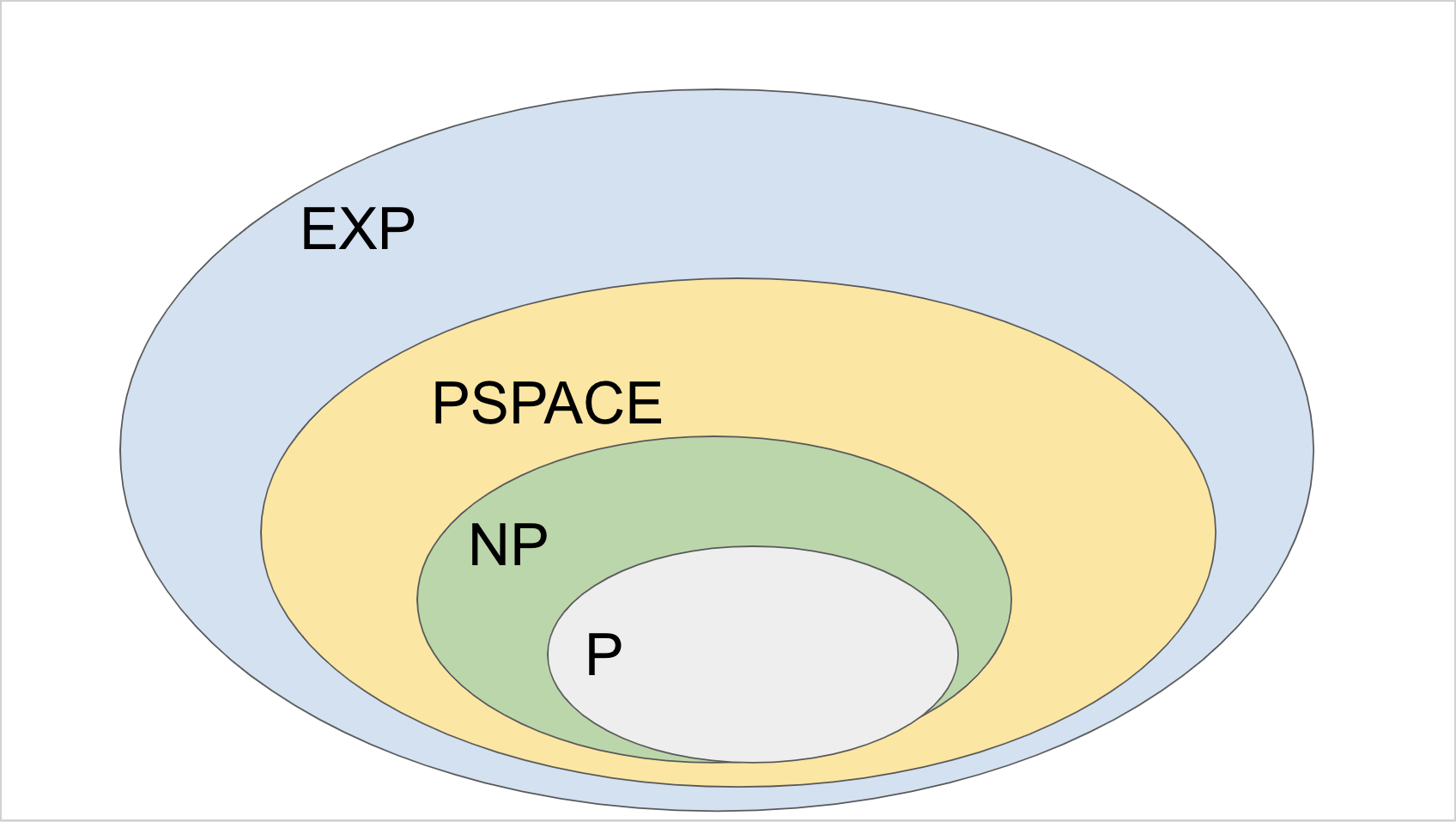
Complexity classes¶
Used to classify and compare computational problems according to the computational resources needed to solve them.
The focus is on decision problems, which are computational problems where for each input there is a binary output ("yes" or "no").
Example: Graph connectivity problem
- Input: graph $G$
- Output: is $G$ connected?
Some complexity classes¶
P - polynomial time¶
Decision problems that can be solved by deterministic algorithms running in time $O(n^c)$ where $n$ is the length of the input.
Captures the notion of efficient classical computation in theoretical computer science.
Examples: graph connectivity, determining if a number is prime, computing shortest paths in a graph
NP - non-deterministic polynomial time¶
Decision problems whose solutions can be verified in polynomial time. If the answer to the input is "yes", then there exists a solution/certificate/proof that is efficiently checkable.
Examples: traveling salesman person problem, boolean satisfiability, factoring.
Most optimization/search problems are in NP. Many are NP complete.
BPP - bounded error probabilistic polynomial time¶
Decision problems that can be solved by a randomized, polynomial time algorithm.
The correct answer must be obtained with high probability (say $99\%$).
Examples: any problem in P, polynomial identity testing
It is conjectured that P = BPP (i.e. randomization does not help for efficient computation).
PSPACE - polynomial space¶
Decision problems that can be solved by a deterministic algorithm that uses $O(n^c)$ bits of space where $n$ is the input length.
Captures the notion of problems that can be solved using a small amount of memory.
Examples: all of P, NP, BPP. Generalized tic-tac-toe, Super Mario Bros.
EXP - exponential time¶
Decision problems that can be solved by a deterministic algorithm that runs in $O(2^{n^c})$ time.
Examples: all of PSPACE, generalized Chess.
BQP - bounded error quantum polynomial time¶
Decision problems that can be solved by a quantum algorithm (i.e. a quantum circuit) of $O(n^c)$ size with high probability.
Captures the notion of efficient quantum computation.
Examples: all of P, BPP, factoring, simulating quantum physics.
Where does BQP live?¶

The central questions¶
- BQP $\subseteq$ BPP?
In other words, is there an efficient classical simulation of quantum computation?
- NP $\subseteq$ BQP?
Can quantum computers be used to solve hard optimization problems like SAT or Traveling Salesperson Problem?
- What are classical upper bounds on BQP?
APPROX-Q-CIRCUIT¶
Definition: The acceptance probability of a quantum circuit $C$ on input $\ket{\psi}$ is the probability that measuring the first qubit of $C\ket{\psi}$ yields $\ket{1}$ (i.e. accepts).
Input: A description of quantum circuit $C$ where either
- $\Pr[ C\ket{0 \cdots 0} \text{ accepts }] \geq .99$
- $\Pr[ C\ket{0 \cdots 0} \text{ accepts }] \leq .01$
Output: Determine which is the case.
APPROX-Q-CIRCUIT is a promise problem because the input is promised to satisfy some condition.
APPROX-Q-CIRCUIT¶
APPROX-Q-CIRCUIT is the canonical BQP complete problem, meaning that it is the "hardest" problem in BQP. If problem $A$ is in BQP, then it can be reduced to an instance of APPROX-Q-CIRCUIT.
In other words, if there is a fast classical algorithm for APPROX-Q-CIRCUIT, then that can be used to solve any problem in BQP.
Claim: APPROX-Q-CIRCUIT is solvable in BQP.
Proof: The description of the circuit $C$ is a list of single- and two-qubit gates $g_1,g_2,\ldots,g_T$ acting on various qubits.
The quantum algorithm to solve APPROX-Q-CIRCUIT is almost tautological: run the gates $g_1,g_2,\ldots$ in sequence, and measure the first qubit of resulting state.
This takes linear* time in the size of the circuit $C$.
* There is some additional overhead due to parsing the description of $C$.
APPROX-Q-CIRCUIT $\in$ EXP¶
The acceptance probability of a quantum circuit can be computed by a classical computer in exponential time.
Proof: Do what we've been doing in class: to compute the result of a circuit, compute the classical description of the state after applying a gate:
$$ \ket{\psi_{t+1}} = g_{t+1} \ket{\psi_t} $$The matrix-vector multiplication takes $(2^n)^2)$ time (if $n$ = number of qubits of $C$). Doing this $T$ times requires $O(T \cdot 2^{2n})$ time.
APPROX-Q-CIRCUIT $\in$ EXP¶
If $\ket{\psi_T} = \sum_{x \in \{0,1\}^n} \alpha_x \ket{x}$, then
$$ \Pr \Big [ C \ket{0 \cdots 0} \text{ accepts} \Big] = \sum_{x \in \{0,1\}^n : x_1 = 1} |\alpha_x|^2 $$Since APPROX-Q-CIRCUIT is BQP-complete, this means BQP $\subseteq$ EXP.
BQP $\in$ PSPACE¶
Quantum computations can also be classically simulated using polynomial space. This is based on the sum-over-histories or Feynman path integral approach.
Key idea: in polynomial space, can iterate over exponentially many possible "histories" or "paths" of a quantum computation, and add up their amplitudes to determine final probability of measuring $\ket{1}$ in output qubit.
Feynman path integral¶
The amplitudes of the output state can be calculated via a tree:
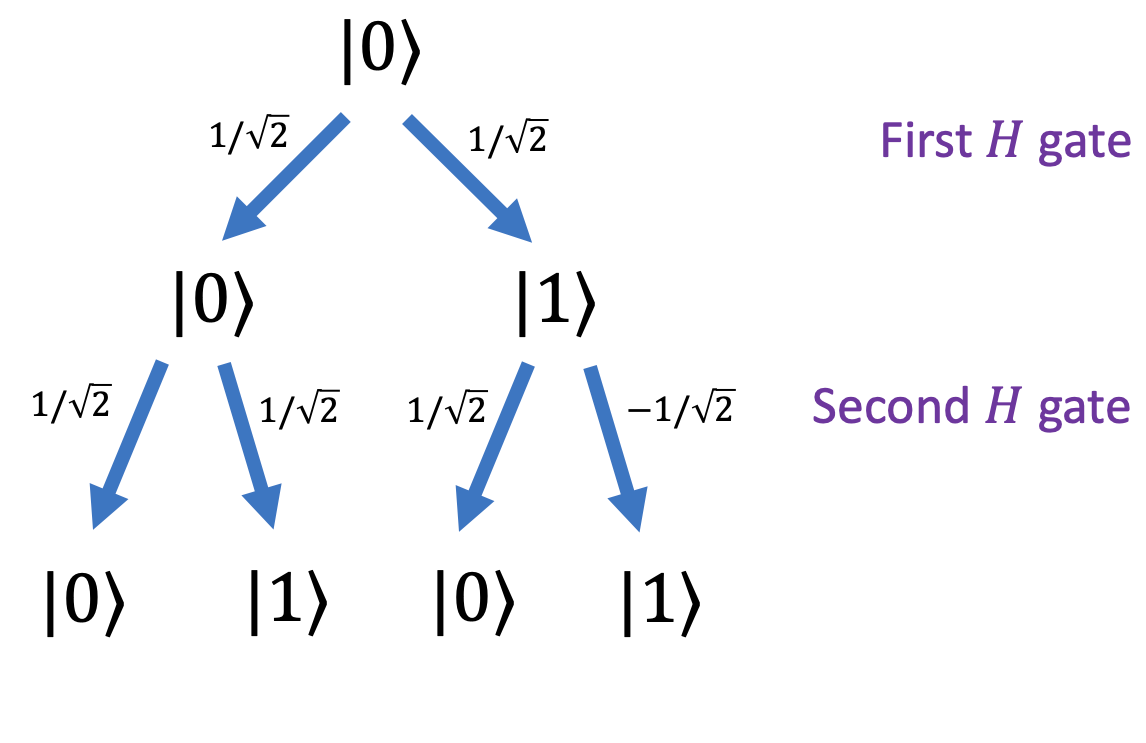
Final amplitude of $\ket{b}$ = sum of amplitudes of all paths from $\ket{0} \to \ket{b}$.
Feynman path integral¶
More generally, suppose we have gates $g_1,g_2,g_3,\ldots,g_T$ in a $n$-qubit circuit.
The computation can be represented by a tree where:
- root node is labelled by $\ket{0 \cdots 0}$
- each node has $2^n$ children labeled by $\ket{x}$ for $x \in \{0,1\}^n$
- edge from node $\ket{x}$ in layer $t$ to node $\ket{y}$ in layer $t+1$ is labeled by transition amplitude $ \bra{y} g_t \ket{x}$
Transition amplitudes¶
Claim: Given $n$-qubit basis states $\ket{x}, \ket{y}$, and two-qubit gate $g$, the transition amplitude $\bra{y} g \ket{x}$ can be computed in (classical) polynomial time.
Proof: Assume without loss of generality that $g$ acts on first two qubits. Then we are really calculating
$$ \bra{y_1 y_2 \cdots y_n} (g \otimes I_{n-2}) \ket{x_1 x_2 \cdots x_n} = \bra{y_1 y_2} g \ket{x_1 x_2} \cdot\langle y_3 y_4 \cdots y_n \mid x_3 x_4 \cdots x_n \rangle $$where $g$ is a $4\times 4$ unitary matrix and $I_{n-2}$ is identity on $n-2$ qubits.
$\bra{y_1 y_2} g \ket{x_1 x_2}$ is the entry of $g$ in row indexed by $(y_1,y_2)$ and column indexed by $(x_1,x_2)$.
ComputeAmp¶
Input: basis states $\ket{x}, \ket{y}$
amp $\leftarrow$ 0
For $u_1$,$u_2$,...,$u_{T-1}\in \{0,1\}^n$:
$\qquad $ amp $ = $ amp $ + \bra{y} g_T \ket{u_{T-1}}$ $ \bra{u_{T-1}} g_{T-1} \ket{u_{T-2}} $ $\cdots \bra{u_1} g_1 \ket{x}$
Return amp
ComputeAmp¶
The subroutine ComputeAmp computes the overall transition amplitude $\bra{y} C \ket{x}$.
It requires $O(T n)$ bits of space to store $u_1,\ldots,u_{T-1}$ and $\mathrm{poly}(n)$ bits to store amp.
It takes $2^{O(Tn)}$ time to loop over all possible paths $(u_1,\ldots,u_{T-1})$.
For each path, updating the amplitude takes polynomial time (because $\bra{u_j} g_j \ket{u_{j-1}}$ is computable in polynomial time).
Polynomial space algorithm for APPROX-Q-CIRCUIT¶
Input: quantum circuit $C$ satisfying promise
prob $\leftarrow$ 0
For all $y \in \{0,1\}^n$ where $y_1 = 1$:
$\qquad$ prob $=$ prob $ + |$ ComputeAmp$(0^n,y)|^2$
If prob $ \geq .99$ then output YES, otherwise output NO
Polynomial space algorithm for APPROX-Q-CIRCUIT¶
The space usage of this algorithm is $\mathrm{poly}(n)$ (to store $y$ and prob) plus whatever ComputeAmp needs, which is polynomial space.
It computes probability of getting $\ket{1}$ in first qubit of final state.
Next time¶
Lower bound for Grover search.