Admin¶
- Pset3 out on Wednesday, due November 2
- Henry, please record the lecture!
Structured speedups¶
So far, we have seen two examples of exponential quantum speedups:
- Simons Algorithm
- Order Finding/Factoring
These speedups are for highly structured problems.
They all use a version of the Quantum Fourier Transform.
Unstructured search problem¶
Given: Oracle access to a black-box function $f: \{0,1\}^n \to \{0,1\}$
Goal: Output a marked input $x$ such that $f(x) = 1$, if one exists.
Classical algorithms need $\Omega(2^n)$ queries to $f$ to find a marked input.
Grover's algorithm¶
Grover's Algorithm can find a marked input with $O(\sqrt{2^n})$ queries to $f$.
Presented by Lov Grover in 1997 in paper called "A fast quantum mechanical algorithm for database search".
This achieves a quadratic speedup. Not as impressive as exponential speedup, but still interesting!
$\text{1 billion}$ seconds $\approx$ 31 years
$\sqrt{\text{1 billion}}$ seconds $\approx$ 9 hours.
Phase vs XOR oracles¶
The Simons and Deutsch algorithms called the oracle via the XOR oracle
$$ U_f \ket{x,b} = \ket{x,b\oplus f(x)}~. $$In Grover's algorithm the oracle is accessed via the Phase oracle
$$ O_f \ket{x} = (-1)^{f(x)} \ket{x}. $$Note that $O_f$ acts on $n$ qubits.
The Phase Oracle can be simulated by one query to the XOR oracle, and XOR oracle can be simulated with one query to the Phase Oracle.
(do on board)
Grover's algorithm¶
For simplicity, let's assume that there exists exactly one marked input.
The circuit:
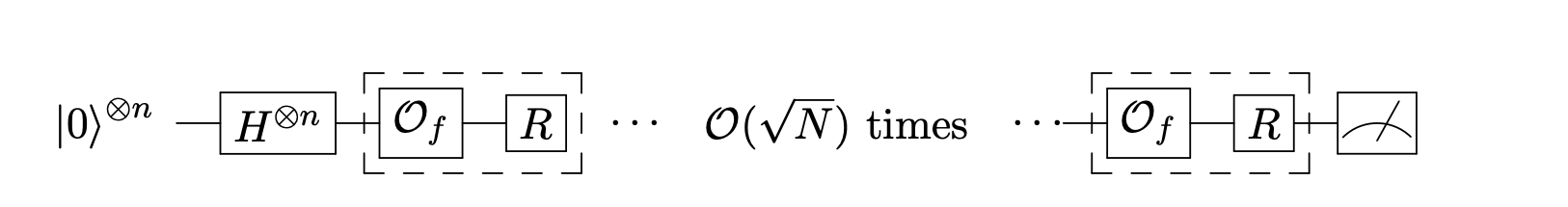
where
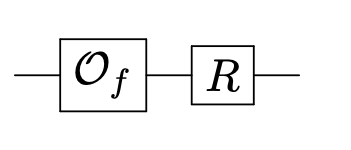
is the Grover iterate.
Grover iterate¶
The state of Grover's algorithm before the Grover iterates is
$$ \ket{+}^{\otimes n} = \frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} \ket{x}. $$The operator $R$ is the $n$-qubit Grover diffusion operator
$$ R = 2 \ketbra{+}{+}^{\otimes n} - I $$Exercise: check that this is unitary!
Analysis of Grover's algorithm¶
Let $x^*$ denote the unique marked input.
Important fact: The intermediate states of Grover's algorithm are linear combinations of
$$ \ket{x^*} \qquad \text{and} \qquad \ket{\Delta} = \frac{1}{\sqrt{2^n - 1}} \sum_{x \neq x^*} \ket{x} $$We can prove this via induction.
Base case (initial state):
$$ \ket{+}^{\otimes n} = \frac{1}{\sqrt{2^n}} \sum_x \ket{x} = \sqrt{\frac{2^n - 1}{2^n}} \ket{\Delta} + \frac{1}{\sqrt{2^n}} \ket{x^*} $$Assume that an intermediate state of Grover's algorithm has form $\ket{\psi} = \alpha \ket{\Delta} + \beta \ket{x^*}$.
Claim: $O_f \ket{\psi}$ is linear combination $\ket{\Delta}, \ket{x^*}$.
Claim: $R \ket{\psi}$ is linear combination of $\ket{\Delta}, \ket{x^*}$.
(do on board)
Analysis of Grover's algorithm¶
(do on board)
Success probability¶
The probability of finding a marked input when measuring the state after $k$ Grover iterations. Running Grover's algorithm for longer can reduce your success probability!
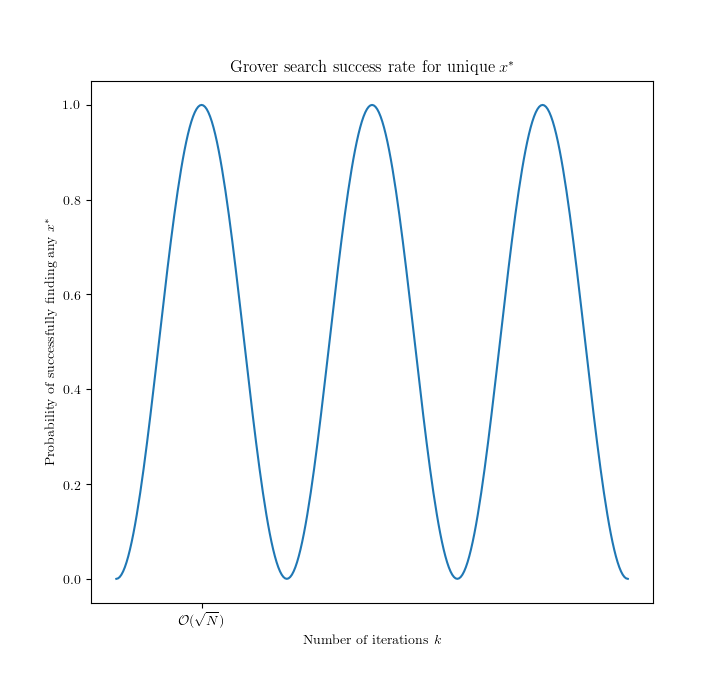
Multiple solutions¶
What happens when there are $M > 1$ solutions to $f(x) = 1$? We can use Grover's algorithm as before, but the success probability curve changes:
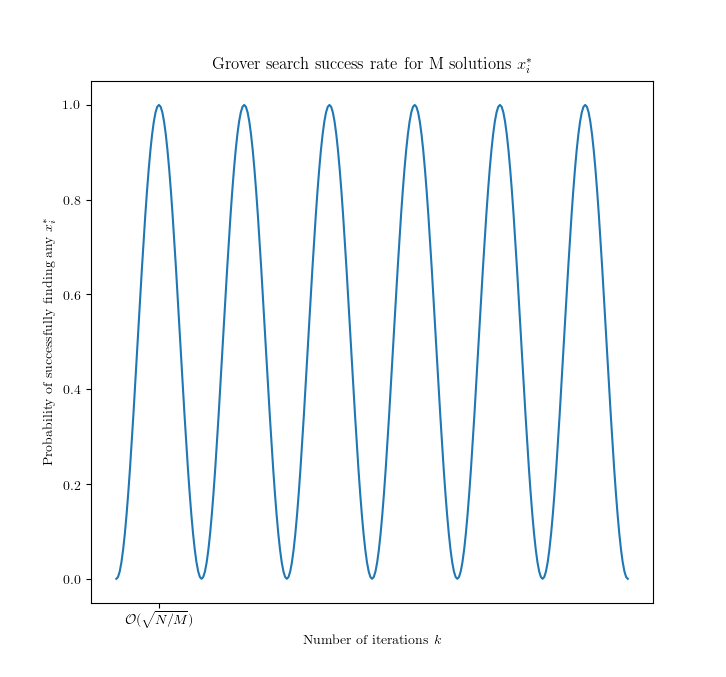
Multiple solutions¶
If the number of solutions $M$ is known, then running $O(\sqrt{N/M})$ iterations will yield a solution with high probability.
If $M$ is unknown, by picking a random number $T$ between $1$ and $\sqrt{N}$ and stopping after $T$ iterations, can find a solution with at least $50\%$ probability. Repeating this $O(1)$ times yields a solution with high probability.
Multiple solutions¶
If $M$ is unknown, then there is a more sophisticated solution to find a solution with $O(\sqrt{N/M})$ queries in expectation.
Idea: try Grover's algorithm with different number of iterations:
$$ T_0, \lambda T_0, \lambda^2 T_0, \ldots $$where $T_0$ is some constant and $1 < \lambda < 4/3$.
Use cases for Grover search¶
Contrary to Grover's original title, "database search" is probably not a good application of Grover's algorithm.
For database search, the oracle $f(x)$ would correspond to something like "If Person $x$ lives in New York City, has blood type O and likes Thai food, output $1$" where $1 \leq x \leq N$.
Although Grover's algorithm makes $O(\sqrt{N})$ queries to $f$, computing $f(x)$ itself may have complexity ~$N=2^n$.
Use cases for Grover search¶
A much better use is when we're trying to solve an abstract search problem where $f(x)$ can be computed much less than $N = 2^n$ time.
Example: Finding satisfying assignments to SAT formulas.
This is an NP complete problem. Believed best classical algorithms takes ~$2^n$ time.
With Grover, can solve it in $O(\sqrt{2^n}) \cdot \mathrm{poly}(n)$ time on a quantum computer.
Next time¶
Quantum algorithms for counting, and amplitude amplification.