Admin¶
- Pset3 out, due November 2
- Henry, please record the lecture!
Recap of Grover search¶
Given query access to $f:\{0,1\}^n \to \{0,1\}$, find a marked input $x$ such that $f(x) = 1$.
- Classical algorithms: Need at least $\sim N$ queries to $f$.
- Grover's algorithm: $\sim \sqrt{N}$ queries suffices.
($N = 2^n$)
Recap of Grover search¶
The algorithm:
- Start with $\ket{+}^{\otimes n}$.
- Run $k = O(\sqrt{N})$ iterations of the Grover iterate
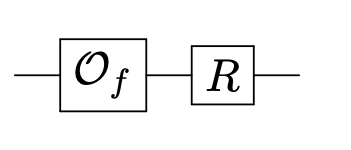
Recap of Grover search¶
The intermediate state of the algorithm lies in the 2-dimensional subspace spanned by
$$ \ket{x^*} \qquad \text{and} \qquad \ket{\Delta} = \frac{1}{\sqrt{N - 1}} \sum_{x \neq x^*} \ket{x}~. $$The Grover iterate operator $R O_f$ rotates states in this subspace by angle $2\theta$ where
$$ \sin \theta = \sqrt{\frac{1}{N}}. $$Multiple solutions¶
If there are $M > 1$ solutions, then can find a solution with $O(\sqrt{N/M})$ queries.
The intermediate states of the algorithm are in the span of
$\ket{\Gamma} = \frac{1}{\sqrt{M}} \sum_{x : f(x) = 1} \ket{x}$, uniform superposition over all solutions
$\ket{\Delta} = \frac{1}{\sqrt{N - M}} \sum_{x : f(x) = 0} \ket{x}$, uniform superposition over all non-solutions
In the end, the output is a random solution.
Multiple solutions¶
What if you wanted to output all solutions?
There is $O(\sqrt{NM})$ query solution:
- Use $\sqrt{\frac{N}{M}}$ queries to find the first solution $x_1$.
- Run Grover search with updated oracle $f_1$ where $x_1$ is excluded. This finds solution $x_2$ with $\sqrt{\frac{N}{M-1}}$ queries.
- Update the oracle to exclude $x_2$. Find another solution $x_3$, etc.
Multiple solutions¶
The total number of queries is
$$ \sqrt{\frac{N}{M}} + \sqrt{\frac{N}{M-1}} + \cdots + \sqrt{\frac{N}{1}} $$Quantum counting¶
What if you wanted to count the number of solutions, not just find them?
Given query access to $f:\{0,1\}^n \to \{0,1\}$, output an estimate $\tilde{M}$ of the number of marked inputs $M$, such that
$$ (1 - \epsilon) M \leq \tilde{M} \leq (1 + \epsilon) M. $$Solution: Grover search + phase estimation.
Quantum counting¶
Recall that for Phase Estimation, we need:
- (Controlled) unitary $U$ (and its powers)
- An eigenvector of $U$
Quantum counting¶
Unitary: we'll use the Grover iterate $G = R O_f$
On the 2-dimensional subspace $\mathrm{span} \{ \ket{\Gamma}, \ket{\Delta} \}$, this is the rotation matrix
$$ \begin{pmatrix} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta \end{pmatrix} $$where $\sin \theta = \sqrt{M/N}$. The eigenvalues of this are $e^{i 2\theta}$ and $e^{-i 2\theta}$.
Quantum counting¶
The nontrivial eigenvectors of $G$ are:
$$ \ket{\psi_{\pm}} = \frac{1}{\sqrt{2}} \Big ( \ket{\Gamma} \pm i \ket{\Delta} \Big). $$We run Phase Estimation with the state $\ket{+}^{\otimes n}$, which satisfies
$$ \ket{+}^{\otimes n} = \alpha \ket{\psi_+} + \beta \ket{\psi_-} $$for some $\alpha,\beta \in \C$.
Quantum counting¶
Running Phase Estimation, we get a state that is close to
$$ \alpha \ket{\psi_+} \ket{\widetilde{2 \theta}} + \beta \ket{\psi_-} \ket{\widetilde{-2 \theta}} $$Measuring the second register, we get an approximation of $2\theta$ or $-2\theta$ with some probability. Assuming $\theta < \pi/2$, we can recover $\theta$ from either.
Using $t$ ancilla qubits, can estimate the phase to within $2^{-t}$.
Quantum counting¶
The estimate of number of solutions is then
$$ \tilde{M} = N (\sin \tilde{\theta})^2. $$How far off is this from the true number of solutions?
Quantum counting¶
$$ \Big | \tilde{M} - M \Big | = N \Big | \sin (\theta + \delta)^2 - \sin(\theta)^2 \Big| $$Quantum counting¶
Thus the estimate satisfies $$ \Big | \tilde{M} - M \Big | \leq 2\sqrt{NM} \delta + N \delta^2 $$
Remember that $\delta \leq 2^{-t}$. Then choosing $t = \log \Big( \frac{1}{\epsilon} \sqrt{\frac{N}{M}} \Big)$ we get
$$ (1 - \epsilon) M \leq \tilde{M} \leq (1 + \epsilon) M. $$as desired.
Complexity of quantum counting¶
We're running phase estimation with $t$ bits of precision, which means we're running $G, G^2, G^4, \cdots, G^{2^t}$ which means
$$ 1 + 2 + 4 + \cdots + 2^t = 2^{t+1} - 1 $$queries to $O_f$.
Complexity of quantum counting¶
This is at most
$$ O \Big (\frac{1}{\epsilon} \sqrt{\frac{N}{M}} \Big) $$queries -- not much more than finding a single solution!
This also gives a way to find a solution without knowing $M$: first get estimate $\tilde{M}$, and then run $O(\sqrt{N/\tilde{M}})$ iterations!
The idea behind Grover's algorithm can be used to solve more general problems! This leads to the Amplitude Amplification algorithm.
Given
- a subspace $S$ of $n$-qubit states,
- a unitary $O$ that recognizes the subspace, meaning
- a unitary $R = 2\ketbra{\phi}{\phi} - I$ for some state $\ket{\phi}$.
Starting with state $\ket{\phi}$, Grover iterations eventually move towards the subspace $S$.
Amplitude amplification¶
We can write $$ \ket{\phi} = \alpha \ket{\phi_S} + \beta \ket{\phi_{S^\perp}} $$
where $\ket{\phi_S} \in S$ and $\ket{\phi_{S^\perp}}$ is orthogonal to $S$.
By running $O(1/\alpha)$ iterations of $O$ followed by $R$, we can obtain a state that has high overlap with $\ket{\phi_S}$.
The algorithm evolves the state in the span of $\ket{\phi_S}$ and $\ket{\phi_{S^\perp}}$.
Grover search, revisited¶
The Grover search algorithm is a special case of amplitude amplification:
- Subspace $S = $ span of all $\ket{x}$ for solutions $f(x) = 1$.
- Unitary $O$ is the phase oracle $O_f$
- $R=2\ketbra{+^n}{+^n} - I$
Application of Amplitude Amplification¶
Let $A$ be a unitary (e.g. corresponding to a quantum circuit). Suppose that
$$ A \ket{0 \cdots 0} = \alpha \ket{\psi_{good}} + \beta \ket{\psi_{bad}} $$where $\ket{\psi_{good}}$ is a good solution. Suppose there is a measurement that yields a good solution with probability $|\alpha|^2$.
What if we want to get a good solution with high probability?
By repeating the circuit $A$ and measurement $T = O(1/|\alpha|^2)$ times, we can get a good solution with high probability.
Using Amplitude Amplification, we can get a good solution with $O(\sqrt{T})$ calls to $A$.
- Let $\ket{\phi} = A \ket{0 \cdots 0}$ denote the initial state.
- Let $O$ denote unitary that recognizes good solutions (i.e. $O \ket{\psi_{good}} = -\ket{\psi_{good}}$).
- Let $R = 2\ketbra{\phi}{\phi} - I = A(2 \ketbra{0}{0} - I)A^\dagger$.
Since the overlap of $\ket{\phi}$ with $\ket{\psi_{good}}$ is $\alpha$, we can boost the amplitude to close to $1$ in $O(1/|\alpha|)$ repetitions.
Next time¶
Quantum complexity theory.