Admin¶
- Two talks by John Preskill this week.
- Henry, please record the lecture!
Last time¶
- Quantum Fourier Transform
Quantum Fourier Transform¶
Quantum algorithm computing the Discrete Fourier Transform unitaries $F_N$, using an $n$-qubit quantum circuit with $\mathrm{poly}(n)$ gates ($N = 2^n$).
$F_N$ maps Fourier basis vector $$ \ket{f_j} = \frac{1}{\sqrt{N}} \sum_{k = 0}^{N-1} \underbrace{\exp \Big( \frac{2\pi i jk}{N} \Big)}_{\omega_N^{jk}} \ket{k} $$ to standard basis vector $\ket{j}$.
Application of QFT: Phase Estimation¶
Phase Estimation Algorithm (PEA) is one of the most important subroutines in quantum computing.
Goal of PEA: Given:
- Ability to run controlled versions of $U, U^2, U^4, \ldots, U^{2^j},\ldots$
- An eigenstate $\ket{\psi}$ where $U \ket{\psi} = e^{2\pi i \theta} \ket{\psi}$,
estimate $\theta$.
How can you estimate a global phase?¶
The eigenvalue $e^{2\pi i \theta}$ looks like a global phase...
...but it becomes a relative phase once you run the controlled-$U$ gate in superposition: \begin{align*} cU \ket{+} \ket{\psi} &= \frac{1}{\sqrt{2}} (\ket{0} \ket{\psi} + \ket{1} U \ket{\psi}) \\ &= \frac{1}{\sqrt{2}} (\ket{0} \ket{\psi} + e^{2\pi i \theta} \ket{1} \ket{\psi}) \\ &= \frac{1}{\sqrt{2}} (\ket{0} + e^{2\pi i \theta} \ket{1}) \ket{\psi} \end{align*}
Phase Estimation Algorithm¶
Assume for simplicity that $\theta$ can be represented using exactly $t$ bits. In other words the binary representation of $\theta$ looks like
$$ \theta = 0.\theta_1 \theta_2 \cdots \theta_t $$where $\theta_1,\theta_2,\ldots \in \{0,1\}$. This is equivalent to
$$ \theta = \frac{\theta_1}{2} + \frac{\theta_2}{2^2} + \cdots + \frac{\theta_t}{2^t}. $$Phase Estimation Algorithm¶
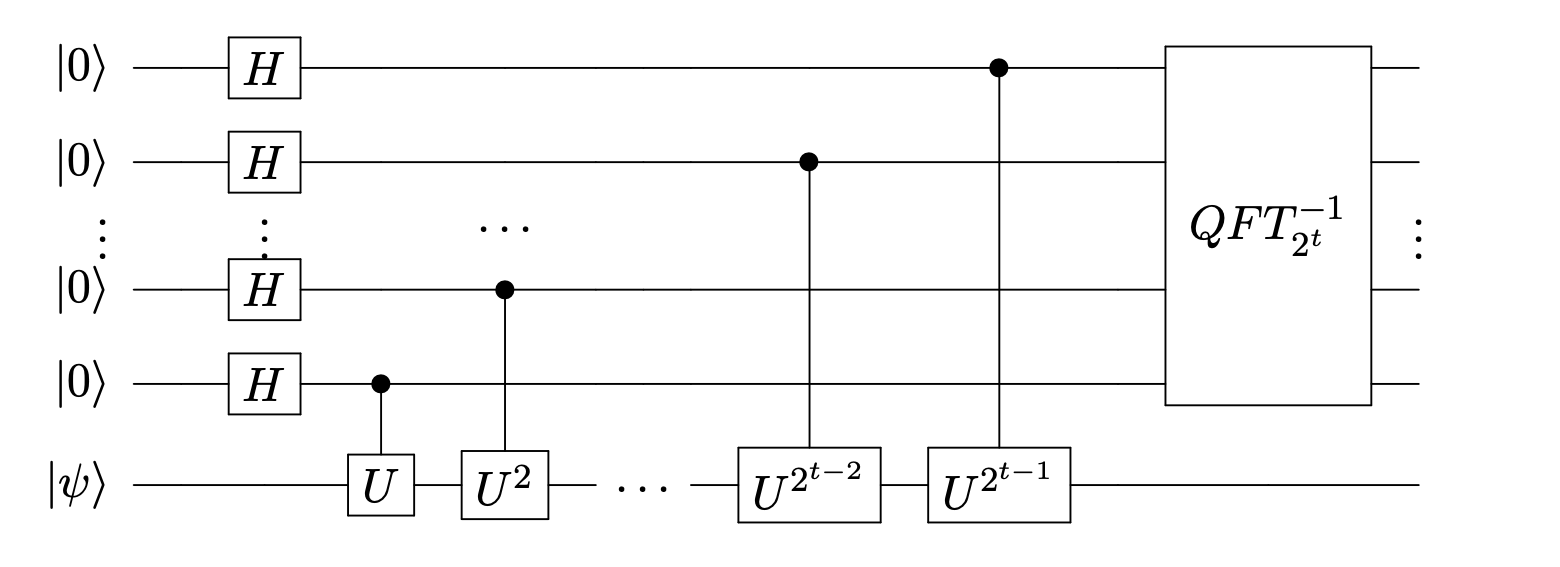
Measuring the first $t$ qubits will yield $\ket{\theta_1,\theta_2,\ldots,\theta_t}$.
Analysis of Phase Estimation Algorithm¶
Let's analyze a special case where $t = 2$, and $\theta = \frac{\theta_1}{2} + \frac{\theta_2}{4}$ for $\theta_1,\theta_2 \in \{0,1\}$.
(On the board...)
Analysis of Phase Estimation Algorithm¶
Question: What if the phase $\theta$ cannot be exactly expressed as $t$ bits?
Answer: If we use $t + k$ ancilla qubits, and measure only the first $t$ ancilla qubits, we will get the best $t$-bit approximation $\widetilde{\theta}$ of $\theta$ with probability $1 - 2^{-k}$.
Analysis of Phase Estimation Algorithm¶
Question: What happens if $\ket{\psi}$ is not an eigenvector of $U$?
Answer: The set $\{ \ket{\phi_j} \}$ of eigenvectors of $U$ forms a basis for $\C^{2^n}$ (if $U$ is $n$-qubit unitary). We can write $\ket{\psi}$ as $$ \ket{\psi} = \sum_j \alpha_j \ket{\phi_j} $$ for some coefficients $\alpha_j$.
Running Phase Estimation on $\ket{\psi}$ with ancilla qubits $\ket{0 \cdots 0}$ yields a state that is close to
$$ \approx \sum_j \alpha_j \ket{\phi_j} \otimes \ket{\widetilde{\theta}_j} $$where $\widetilde{\theta}_j$ is an approximation of the eigenphase $\theta_j$, i.e. $U \ket{\phi_j} = e^{2 \pi i \theta_j} \ket{\phi_j}$.
Measuring the last register yields $\widetilde{\theta}_j$ with probability $|\alpha_j|^2$.
Applications of Phase Estimation¶
- Shor's Factoring Algorithm
- Simulation of Quantum Systems
- Quantum Algorithms for Optimization
RSA, Factoring, and Ordering Finding¶
RSA Cryptosystem¶
- Invented by Rivest, Shamir, and Adleman in 1977
- Most widely deployed public-key cryptosystem
- Enables public-key encryption as well as digital signatures
Public-key encryption¶
- Bob generates a secret-key/public-key pair $(sk,pk)$, and publishes $pk$ on the internet.
- Alice uses $pk$ and her message $m$ to create a ciphertext $c$ which she sends to Bob.
- Bob gets $c$, and uses $sk$ to decode $m$.
- The adversary sees $(pk,c)$, and should get no information about $m$.
- Pick random prime number $1 \leq e \leq (p-1)(q - 1)$.
- Compute integer $d$ where $ed = 1$ mod $(p-1)(q-1)$.
- Set public key $pk = (e,N)$, and secret key $sk = d$.
RSA Cryptosystem¶
Alice gets a message $1 \leq m < N$. She computes and send $c = m^e$ mod $N$, and send $c$ to Bob.
Bob computes $m' = c^d$ mod $N$ to decode the message.
This works because $c^d = (m^e)^d = m^{ed}$, and modulo $N$ this equals $m$ by Fermat's Little Theorem.
RSA Cryptosystem¶
Adversary sees the public key $pk = (e,N)$ and the encrypted message (ciphertext) $c$.
It does not know the primes $p,q$, nor the secret key $sk = d$.
If it knew the prime factorization $N = pq$ it could compute the secret key!
RSA Cryptosystem¶
In other words, if the adversary can factor large integers very quickly, then it can break the security of the RSA cryptosystem).
(It's an open question of whether breaking RSA necessarily means being able to factor!)
Factoring Problem¶
Input: Positive integer $N$.
Output: Prime factorization of $N$ as $p_1^{a_1} p_2^{a_2} \cdots$.
The prime factorization of $N$ is unique by the Fundamental Theorem of Arithmetic.
To find a factorization of $N$, it suffices to be able to find some nontrivial divisor of $N$.
Factoring Problem¶
It is widely believed that Factoring is hard for classical computers. The best classical algorithm, known as the General Number Field Sieve, takes time roughly $$ \exp \Big( O (\log N)^{1/3} \Big)~. $$
This is essentially exponential in the number of digits of $N$.
Shor's Algorithm¶
A quantum algorithm to solve Factoring in $\mathrm{poly}(\log N)$ steps.
Discovered by Peter Shor in 1993. He was inspired by Simon's Algorithm.
Shor's Algorithm is also a hybrid classical-quantum algorithm.
- Classical part: reduce the factoring problem to order finding.
- Quantum part: solve order finding.
Order Finding¶
Input: given positive integers $N,x$ such that
- $1 \leq x < N$
- $gcd(N,x) = 1$ (i.e. they do not have any nontrivial factors in common)
Output: find smallest integer $r$ such that $x^r = 1$ mod $N$ (called the order of $x$ mod $N$).
Reducing Factoring to Order Finding¶
Goal: we want to find a nontrivial divisor of $N$, assuming ability to solve Order Finding.
- Pick a random $1 \leq x < N$. If $gcd(N,x) \neq 1$, great! We've found a nontrivial factor of $N$.
- Otherwise, $gcd(N,x) = 1$. Compute the order of $x$ mod $N$; call this $r$.
- If $r$ is odd, go back to Step 1.
Reducing Factoring to Order Finding¶
- If $r$ is even, then $x^r - 1 = 0$ mod $N$ and
If $a, b$ are multiples of $N$, go back to Step 1.
- Otherwise, we have found integers $a,b$ such that
Since $a,b$ are not multiples of $N$, computing $gcd(a,N)$ or $gcd(b,N)$ will yield a nontrivial divisor.
Next time¶
A quantum algorithm to solve Order Finding