Admin¶
- Pset2 due Sunday, October 9, 11:59pm.
- Henry, please record the lecture!
Last Time¶
- Holevo's Theorem, Superdense coding, Universal gate sets and the Deutsch algorithm
Deutsch problem and the Deutsch algorithm¶
Deutsch problem: Given oracle access to a boolean function $f: \{0,1\} \to \{0,1\}$, decide whether $f(0) = f(1)$ or $f(0) \neq f(1)$.
Deutsch algorithm:

This quantum algorithm solves the Deutsch problem with one call to $U_f$, which maps $\ket{x,b}$ to $\ket{x, b \oplus f(x)}$.
Deutsch algorithm¶
The algorithm evaluates the function $f$ in superposition. This seems to give a 2x speedup!
Is this cheating? Maybe the "quantum access" is just really making multiple classical queries under the hood?
Deutsch algorithm¶
Observation: the qubit storing the answer at the end corresponds to the input wire of the oracle $U_f$. We don't care about the output wire!
This is a common feature in many quantum algorithms with exponential speedup.
Simons problem¶
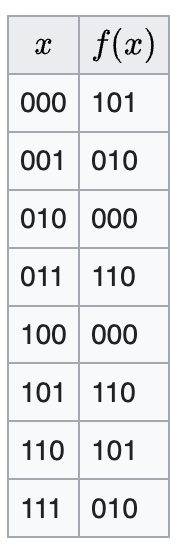
Problem: Given oracle access to $f:\{0,1\}^n \to \{0,1\}^n$ such that there exists a nonzero secret string $s \in \{0,1\}^n$ where for all $x, y \in \{0,1\}^n$
$$ f(x) = f(y) \Leftrightarrow x \oplus y = s. $$find the secret string $s$.
Simons problem¶
Problem: Given oracle access to $f:\{0,1\}^n \to \{0,1\}^n$ such that there exists a nonzero secret string $s \in \{0,1\}^n$ where for all $x, y \in \{0,1\}^n$
$$ f(x) = f(y) \Leftrightarrow x \oplus y = s. $$find the secret string $s$. Here $x \oplus y$ means bitwise XOR.
Question: How many queries to $f$ are necessary to find the secret?
A classical algorithm to find the secret¶
- Randomly sample $x_1,\ldots,x_K \in \{0,1\}^n$ for $K = 10 \sqrt{2^n}$.
- Check if there exists a pair $x_i \neq x_j$ where $f(x_i) = f(x_j)$. If so, then output $s = x_i \oplus x_j$.
By the birthday paradox, this algorithm will find the secret with high probability. Requires $O(2^{n/2})$ queries to $f$. (Show on board)
$2^{n/2}$ queries are necessary for any classical algorithm!
Simons algorithm¶
A quantum algorithm queries $f$ by calling the $2n$-qubit unitary $U_f$ that maps
$$| \underbrace{x}_{n \text{ qubits}}, \underbrace{z}_{n \text{ qubits}} \rangle \mapsto \ket{x, z \oplus f(x)}$$Here, $\oplus$ denotes bitwise addition.
Simons algorithm¶
Simons algorithm is a classical-quantum hybrid algorithm.
It uses the quantum computer as a subroutine to sample from a distribution many times, and uses classical post-processing to extract the secret.
Simons subroutine: Quantum circuit queries $U_f$ once and obtains a uniformly random string $y \in \{0,1\}^n$ where inner product of $y$ and the secret $s$,
$$ s \cdot y = s_1 y_1 \oplus s_2 y_2 \oplus \cdots \oplus s_n y_n $$is equal to $0$.
Simons algorithm, classical post-processing¶
Classical post-processing:
Obtain $m = 100n$ samples $y^{(1)}, y^{(2)}, \ldots,y^{(m)}$ such that
\begin{align*} y^{(1)} \cdot s &= 0 \\ y^{(2)} \cdot s &= 0 \\ &\vdots \\ y^{(m)} \cdot s &= 0 \end{align*}With high probability, can solve this system of linear equations using Gaussian elimination to get $s$.
What is $H^{\otimes n} \ket{0}^{\otimes n}$?
This can be rewritten as $(H \ket{0})^{\otimes n} = \ket{+}^{\otimes n}$.
This is equivalently $$ \ket{+}^{\otimes n} = \Big (\frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1} \Big)^{\otimes n} = \frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} \ket{x_1,\ldots,x_n} $$
What is $H^{\otimes n} \ket{x_1,\ldots,x_n}$?
This is $$ (H \ket{x_1}) \otimes (H \ket{x_2}) \otimes \cdots \otimes (H \ket{x_n}) = \\ \frac{1}{\sqrt{2^n}} \Big( \ket{0} + (-1)^{x_1} \ket{1} \Big) \otimes \Big( \ket{0} + (-1)^{x_2} \ket{1} \Big) \otimes \cdots \otimes \Big( \ket{0} + (-1)^{x_n} \ket{1} \Big) $$
Expanding out, we get $$ = \frac{1}{\sqrt{2^n}} \sum_{y \in \{0,1\}^n} (-1)^{x_1 y_1 + x_2 y_2 + \cdots + x_n y_n} \ket{y_1,\ldots,y_n} \\ = \frac{1}{\sqrt{2^n}} \sum_{y \in \{0,1\}^n} (-1)^{x \cdot y} \ket{y} $$
Simons algorithm¶
- Makes $O(n)$ queries to $U_f$ and solves the problem with high probability
- Once again, the valuable information is stored not in the answer register of $U_f$, but in the input register.
Simons algorithm¶
- Making crucial use of constructive/destructive interference!
- It's finding global hidden structure in the function.
- Is this speedup more convincing?
Simons algorithm¶
Invented by Dan Simons in 1992, and was the first example of a problem that could be solved exponentially faster with a quantum algorithm compared to a classical randomized algorithm.
This algorithm directly inspired Peter Shor to invent the famous factoring algorithm.
Recently, Simons algorithm also has applications to breaking symmetric key cryptography.
Next time¶
Quantum Fourier Transform