Admin¶
- Pset2 due Sunday, October 9, 11:59pm.
- Henry, please record the lecture!
Last Time¶
- EPR Paradox, Bell's theorem, CHSH game
How much information do qubits store?¶
An $n$-qubit state $\ket{\psi}$ on the surface looks like it contains exponential amounts of information, because it is represented by a vector of dimension $2^n$.
In quantum computing/quantum mechanics, we want to harness this to our advantage.
But as mentioned before, there's a tension between the exponentiality of quantum states, and the fact that this is hidden behind a veil of measurement.
Holevo's Theorem¶
If we have $n$ qubits, how much classical information can we store? Can we use $n$ qubits as a "quantum hard drive" to store many more than $n$ classical bits?
No! Holevo's theorem states that, for the purposes of information storage, quantum bits are no better than classical bits!
Holevo's Theorem¶
Alice has an $m$-bit string $X$ that she wants to transmit to Bob. She wants to encode $X$ into some $n$-qubit quantum state $\ket{\psi_X}$ such that Bob can perform some computation (unitaries + measurement) to try to decode $X$.
Bob only gets $X$ with high probability if the number of qubits $n$ is at least $m$.

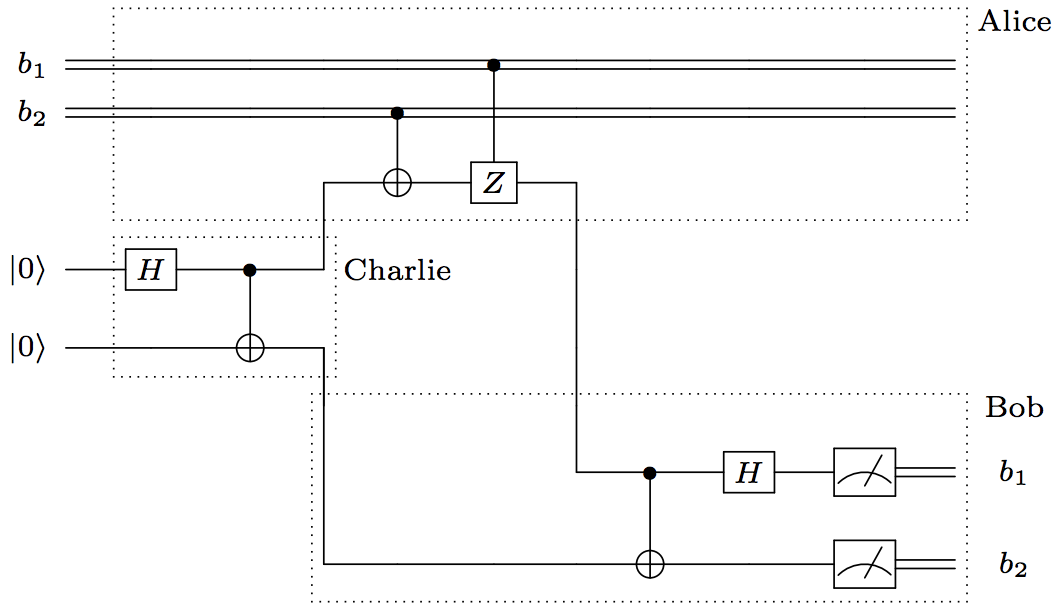
Superdense Coding¶
Using preshared entanglement, Alice can save on the number of qubits she sends to convey $X$. This is achieved by a protocol known as superdense coding.
This allows Alice to convey $m$ classical bits, while sending only $n = m/2$ qubits to Bob, provided they use preshared entanglement.
A simple equation describing superdense coding:
$$ 1 \text{ebit} + 1 \text{qbit} = 2 \text{cbits}. $$On the other hand, teleportation can be thought of as:
$$ 1 \text{ebit} + 2 \text{cbits} = 1 \text{qbit}. $$The protocol for superdense coding is very similar to teleportation. An EPR pair is shared (prepared by Charlie) is shared by Alice and Bob. Alice gets two bits $(b_1,b_2)$, which determines which operations she applies to her qubit.
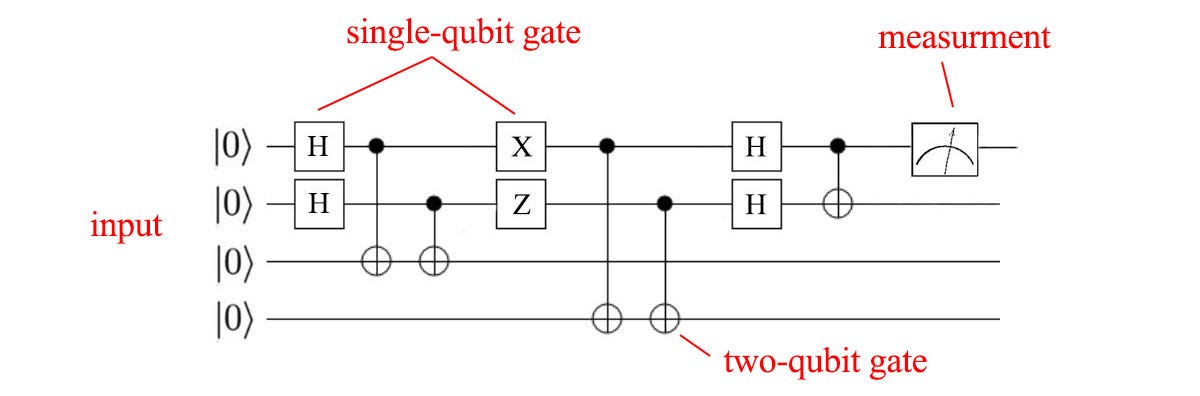
Quantum Computation¶
What is quantum computation?¶
It's whatever you can do with a quantum circuit, where (typically):
- The input qubits start in the $\ket{0}$ state.
- A sequence of single and two-qubit gates drawn from a Gate Set
- Measurements (usually at the end)
Gate sets¶
What single- and two qubit gates are allowed in a quantum circuit?
It depends on the hardware!
A gate set $\mathcal{G}$ is called universal if, for any unitary $U$ (which may act on many qubits), one can construct a circuit using gates from $\mathcal{G}$ to approximate $U$.
Notion of approximation¶
Definition: We say that unitary $U$ $\epsilon$-approximates $V$ if for all quantum states $\ket{\psi}$,
$$ \Big \| U \ket{\psi} - V \ket{\psi} \Big \| \leq \epsilon. $$A circuit $C$ without measurements corresponds to some unitary, so it is meaningful to say that a circuit $C$ approximates a unitary matrix.
Universal gate sets¶
A continuous universal gate set: Rotations $$ R_X(\theta) = \begin{pmatrix} \cos \theta & -i \sin \theta \\ -i \sin \theta & \cos \theta \end{pmatrix} \qquad R_Y(\theta) = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}$$ $$ R_Z(\theta) = \begin{pmatrix} e^{- i \theta} & 0 \\ 0 & e^{i \theta} \end{pmatrix} $$ over all $0 \leq \theta \leq 2\pi$ plus Phase shift $$ P(\varphi) = \begin{pmatrix} 1 & 0 \\ 0 & e^{i \varphi} \end{pmatrix} $$ over all $0 \leq \varphi \leq 2\pi$ plus CNOT
Universal gate sets¶
A discrete, finite universal gate set: $$ H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \qquad S = \begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix} \qquad CNOT $$ and $$ T = \begin{pmatrix}1 & 0 \\ 0 & e^{i \pi /4} \end{pmatrix} $$
Universal gate sets¶
Using a universal gate set $\mathcal{G}$ means, in principle we don't have to worry about what gates are used by a given quantum circuit $C$.
That's because there is a way to compile the circuit $C$ into another circuit $C'$ that uses only gates from $\mathcal{G}$, and $C$ approximates $C'$.
Ideally, we'd like the compiled circuit $C'$ to be not much bigger than $C$.
Solovay-Kitaev Theorem¶
Let $\Gamma \subseteq \mathrm{SU}(2)$ (i.e. the set of single-qubit unitaries up to a global phase). Suppose
- $\Gamma$ generates a dense subgroup of $\mathrm{SU}(2)$.
- $\Gamma$ is closed under inverse.
Then for all $\epsilon > 0$ any unitary $U \in \mathrm{SU}(2)$ can be $\epsilon$-approximated by a product of at most $O(\log (\frac{1}{\epsilon}))$ gates from $\Gamma$.
Universal gate sets¶
Corollary: Let $\Gamma \subseteq \mathrm{SU}(2)$ denote a set of single qubit unitaries satisfying conditions of Solovay-Kitaev theorem (an example is the set $\{ H, T \}$). Then for all $n$, for all circuits $C$ (allowed to use any single and two-qubit gates), for all $\epsilon > 0$
There exists a circuit $C'$ consisting of gates from $\Gamma \cup \{ CNOT \}$ only that
- $\epsilon$-approximates $C$
- number of gates in $C'$ is at most number of gates in $C$ times $O(\log (1/\epsilon))$.
Quantum circuit synthesis¶
In quantum computing, we often want to come up with a quantum circuit $C$ to (approximately) implement some unitary $U$. Hopefully, the circuit $C$ is not too large! This is called quantum circuit synthesis.
How many single- and two-qubit gates are needed to build a circuit $C$ that approximates a given unitary $U$?
In general, at least $4^n$!
Our first quantum algorithm¶
Deutsch problem¶
Given oracle access to a boolean function $f: \{0,1\} \to \{0,1\}$, decide whether $f(0) = f(1)$ or $f(0) \neq f(1)$.
Oracle access to a function $f$ means that the computer can only access it as a black-box, i.e., query some inputs, and get the corresponding outputs. The computer cannot access how the black box is implemented.
Claim: Any classical algorithm that solves the Deutsch problem must make $2$ queries to $f$.
Quantum oracles¶
Quantum algorithms can access a black-box function $f$ through a unitary $U_f$ corresponding to the reversible version of $f$. For $f:\{0,1\} \to \{0,1\}$, this is a two-qubit unitary $$ U_f \ket{x, b} = \ket{x, b \oplus f(x)}. $$ A quantum circuit that wants to access $f$ will simply call $U_f$ just like any other two-qubit gate.
Deutsch algorithm¶

This quantum algorithm solves the Deutsch problem with one call to $U_f$. Let's analyze this on the board.
Deutsch algorithm¶

If $f(0) = f(1)$, output qubit always measures to $\ket{0}$.
If $f(0) \neq f(1)$, output qubit always measures to $\ket{1}$.
Deutsch algorithm¶
The algorithm evaluates the function $f$ in superposition. This seems to give a 2x speedup!
Is this cheating? Maybe the "quantum access" is just really making multiple classical queries under the hood?
Next time: Exponential speedups¶
- Deutsch-Josza Algorithm
- Simons Algorithm