Admin¶
- Pset2 due Sunday, October 9, 11:59pm.
- If you had trouble with printing to PDF, come to Henry's office hours on Tuesday 4pm to debug this.
- Quantum Distinguished Speaker Series: John Preskill (October 13)
- Henry, please record the lecture!
Last Time¶
Measurements in different bases
Heisenberg Uncertainty Principle
EPR Paradox
EPR Paradox¶
Einstein, Podolsky, and Rosen's thought experiment about the EPR pair: $$ \frac{1}{\sqrt{2}} \Big ( \ket{ 00 } + \ket{11} \Big) $$
If Alice measures in the standard basis and gets outcome $\ket{b}$, Bob's qubit will collapse to $\ket{b}$.
Otherwise, if Alice measures in the diagonal basis and gets outcome $\ket{+}$ or $\ket{-}$, Bob's qubit will collapse to that state too.
Faster-than-light communication?¶
It sounds like measurement causes the state of far-away qubits to change instantly. Can this be a mechanism to communicate instantly to distant parts of the universe?
No! Alice, given her measurement outcome, knows the state of Bob's qubit. But she cannot control the outcome; it's random.
Since it's random, and Bob does not know the outcome, he cannot predict the state of his qubit.
EPR Paradox continued¶
Alice and Bob always get the same outcomes if they measure in the same basis. To EPR, this seems to violate Heisenberg's Uncertainty Principle.
EPR proposed that Quantum Mechanics be replaced with a local hidden variable theory. This should be
- Consistent with QM
- Not allow faster-than-light communication
- All measurement outcomes are described by hidden, underlying variables.
Bell's Theorem¶

John Bell (1964): No local hidden variable theory can be compatible with Quantum Mechanics!
He devised an experiment, nowadays called a Bell test, such that the predictions of Quantum Mechanics differ from the predictions of any local hidden variable theory!
CHSH Game¶
A simplification of Bell's experiment, devised in 1970s by Clauser, Horne, Shimony, Holt.
Setup:
- Two cooperating, but separated players Alice and Bob.
- Referee who plays game with Alice and Bob.
CHSH Game¶
- Referee flips two coins to get random bits $x,y \in \{0,1\}$
- Sends $x$ to Alice, $y$ to Bob.
- Alice responds with bit $a$, Bob responds with bit $b$.
- Alice, Bob win if $a \oplus b = x \wedge y$
CHSH Game¶
Put another way:
| $x$ | $y$ | Win condition |
|---|---|---|
| $0$ | $0$ | $a = b$ |
| $0$ | $1$ | $a = b$ |
| $1$ | $0$ | $a = b$ |
| $1$ | $1$ | $a \neq b$ |
What is maximum win probability for Alice and Bob?
CHSH Game: Deterministic Alice and Bob¶
Suppose Alice and Bob are deterministic.
This means Alice's answer $a$ is a fixed function $a(x)$ of her question. Similarly, Bob answers with a function $b(y)$.
One can see, by trying all possible functions for Alice/Bob, the maximum win probability is $3/4$.
What's a simple deterministic strategy that achieves $3/4$?
CHSH Game: LHV Alice and Bob¶
Suppose Alice and Bob are described by local hidden variables.
This means that there is an underlying random variable $\lambda$, such that
- Before the game starts, $\lambda$ is sampled from some distribution $\mathcal{L}$
- Questions $(x,y)$ sampled independently of $\lambda$.
- Alice's answer is a function $a(x,\lambda)$
- Bob's answer is a function $b(y,\lambda)$
What is maximum win probability for Alice and Bob?
CHSH Game: LHV Alice and Bob¶
Being able to use hidden random variable $\lambda$ does not help Alice and Bob: their maximum win probability is $3/4$.
Proof: $$ \Pr [ \text{win} ] = \sum_\lambda \Pr[\lambda] \cdot \Pr[ \text{win} \mid \lambda]$$ But if $\lambda$ is fixed, then Alice and Bob's answers are deterministic functions of their questions only, meaning $\Pr[\text{win} \mid \lambda] \leq \frac{3}{4}$. Therefore $$ \Pr [ \text{win} ] \leq \sum_\lambda \Pr[\lambda] \cdot \frac{3}{4} \leq \frac{3}{4}. $$
CHSH Game: LHV Alice and Bob¶
In other words, Einstein would've predicted that Alice and Bob cannot win with probability greater than $3/4$ in the CHSH game!
CHSH Game: Quantum Alice and Bob¶
What does Quantum Mechanics predict?
There exists a quantum strategy involving quantum entanglement where Alice and Bob win with probability $\approx 85.5\%$.
This gives an experiment to rule out local hidden variable theories!
CHSH Game: Quantum Alice and Bob¶
- Before the game starts, Alice and Bob get together and generate an EPR pair
Alice takes one qubit and Bob takes another qubit, and they go their separate ways.
- When players get their question, they measure their qubit in a basis to get a binary outcome which they map to $0$ or $1$ as their answer.
CHSH Game: Quantum Alice and Bob¶
Alice's measurements on her qubit, depending on her question $x$:
| $x=0$ | $x=1$ |
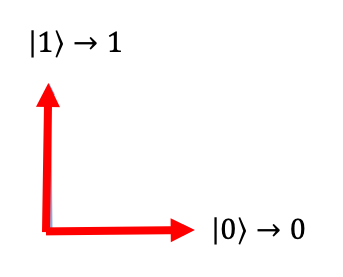 |
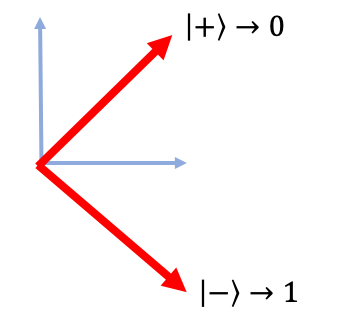 |
CHSH Game: Quantum Alice and Bob¶
How well does this strategy do? Suppose $x = 0, y= 0$.
Alice measures her qubit in standard basis. Bob measures using
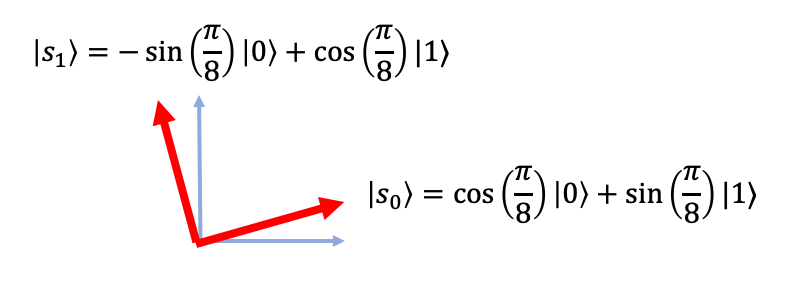
In order to win, Alice and Bob's answers must match.
How to analyze two simultaneous measurements on two separate qubits?
We can pretend Alice measures first, and then Bob. Or vice versa! Distributions of outcomes are identical.
What happens when Alice measures her qubit of EPR pair in standard basis?
Alice gets $\ket{0}$ with probability $\frac{1}{2}$, and joint state collapses to $ \ket{0} \otimes \ket{0}$.
To win, Bob must measure his qubit and get $\ket{s_0}$ outcome.
Since his qubit is now in $\ket{0}$ state, he gets this outcome with probability $$ \Big | \langle 0 \, \Big | \, s_0 \rangle \Big|^2 = \cos^2(\pi/8) \approx .8535\ldots $$
On the other hand, Alice gets $\ket{1}$ with probability $\frac{1}{2}$, and joint state collapses to $ \ket{1} \otimes \ket{1}$.
To win, Bob must measure his qubit and get $\ket{s_1}$ outcome.
Since his qubit is now in $\ket{1}$ state, he gets this outcome with probability $$ \Big | \langle 1 \, \Big | \, s_1 \rangle \Big|^2 = \cos^2(\pi/8) \approx .8535\ldots $$
In either case they win with probability $\cos^2(\pi/8) \approx .8535\ldots$.
CHSH Game: Quantum Alice and Bob¶
One more example: suppose $x = 1, y= 1$.
Alice measures her qubit in diagonal basis. Bob measures using
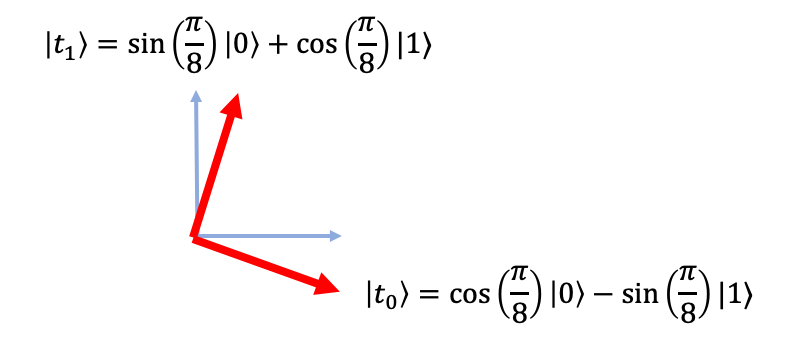
In order to win, Alice and Bob's answers must differ.
If Alice measures $\ket{+}$, then state collapses to $\ket{+} \otimes \ket{+}$ and Bob must measure $\ket{t_1} = \sin(\pi/8) \ket{0} + \cos(\pi/8) \ket{1}$ to win. This occurs with probability:
$$ \Big | \langle + \, \Big | \, t_1 \rangle \Big|^2 = \cos^2(\phi) $$where $\phi$ is the angle between $\ket{+}$ and $\ket{t_1}$.
If Alice measures $\ket{+}$, then state collapses to $\ket{+} \otimes \ket{+}$ and Bob must measure $\ket{t_1} = \sin(\pi/8) \ket{0} + \cos(\pi/8) \ket{1}$ to win. This occurs with probability:
$$ \Big | \langle + \, \Big | \, t_1 \rangle \Big|^2 = \cos^2(\pi/8) \approx .8535\ldots $$where $\pi/8$ is the angle between $\ket{+}$ and $\ket{t_1}$.
If Alice measures $\ket{-}$, then state collapses to $\ket{-} \otimes \ket{-}$ and Bob must measure $\ket{t_0} = \cos(\pi/8) \ket{0} - \sin(\pi/8) \ket{1}$ to win. This occurs with probability:
$$ \Big | \langle - \, \Big | \, t_0 \rangle \Big|^2 = \cos^2(\pi/8) \approx .8535\ldots $$CHSH Game: Quantum Alice and Bob¶
Checking the other two cases ($x=1,y=0$ and $x=0,y=1$), you see the they always win with probability $\cos^2(\pi/8) \approx .854\ldots$. This shows that there is quantum advantage for the players in the CHSH game!
It turns out that $\cos^2(\pi/8)$ is the best win probability for quantum strategies
The quantum advantage in the CHSH game comes from the players' entanglement.
Local measurements on entangled states give rise to correlations that are stronger than any classical correlations.
These correlations are often called nonlocal.
Experimental confirmation of Bell's Theorem¶
Over the years, many experiments conducted of Bell's Theorem (these are called Bell tests).
Starting in 1972, many tests (some based on CHSH game, others different) conducted. All demonstrate winning probabilities that cannot be explained by any LHV.
Conclusion:
- Quantum mechanics is fundamentally a non-classical theory, and Nature seems to be Quantum Mechanical.
- Nature is intrinsically probabilistic.
Experimental confirmation of Bell's Theorem¶
Next time¶
Quantum computing: Universal gate sets, and a (modest) quantum speedup
